| Benævnelser |
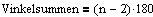grader
|
Et polygon består af sider og vinkelspidser.
Et vilkårligt polygon kan med n kanter kan inddeles i n-2 trekanter |
|
|
|
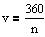grader
|
Et regulært polygon er en n-kant hvis sider er lige lange og hvis vinkler er lige store.
Inddeles et regulært polygon i n-2 trekanter vil trekanternes fælles skæringspunkt være centrum i polygonet, der ligeledes er centrum i de indskrevne- og omskrevne cirkler. Trekanternes vinkelspids mod centrum i polygonet har vinklen:
|
|
|
Vinkelspidser bevævnes med på hinanden følgende kapitalære bogstaver som f.eks. A, B, C
Sider benævnes med ikke kapitalære udgaver af den modståendes sides bogstav. F.eks. a,b,c.
Dog kan sider også benævnes AB i stedet for c osv.
En højde er normal til en side og går til modstående vinkelspids.
|
|
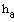
Højder navngives h mærket med bogstavet hvortil de er associeret.
|
|
|
Medianer forbinder en vinkelspids med modstående sides midtpunkt.
|
|
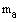
Medaner benævnes m mærket med det bogstav hvortil de er assicieret.
|
|
|
Vinkelhalveringslinjer udgår fra en vinkelspids således at den halverer vinkelspidsens linjer.
Trekantens vinkelhalveringslinjer skærer hinanden i samme punkt, som også danner centrum for trekantens indskrevne cirkel.
Diagonaler forbinder to modstående vinkelspidser og forefindes aldrig i trekanter og andre polygoner med et ullige antal side.
|
| Trekanter |
|
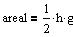
Dette gælder for en retvinklet trekan
|
|
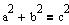
ytagoras formel for retvinklede
trekante
|
|
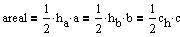
Den vilkårlige trekants area
|
| Firkanter |
| Kvadratet |
|
|
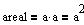
| Retangel |
|
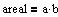
I et rektangel er hvert sidepar lige langt, diagonalerne er lige lange og kantvinklerne er 90 grader.
|
| Rombe |
|
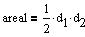
Alle sider i en rombe er lige lange. Modstående vinkler er lige store og diagonalerne er normale til hinanden.
|
| Paralelogram |
|
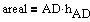
Sideparene er lige lange og diagonalerne halverer hinanden
|
| Trapez |
|
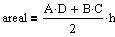
I et trapez er to sider parallelle, hvorimellem højden h forefindes.
|
