| Determinantmetoden
til at løse to ligninger med to ubekendte |
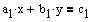
|
Ligningerne skal opstilles på denne grundform
|
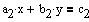
|
|
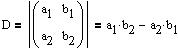
|
Nu findes determinanteme
|
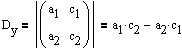
|
|
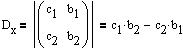
|
|
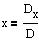
|
Resultaterne findes som følgende
|
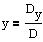
|
|
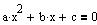
|
Løsning af andengradsligninger
Andengradsligningens grundform
|
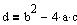
|
Diskriminanten findes
|
|
|
De tre løsningstilfælde:
|
| Hvis d = 0
|
Én løsning: parablens toppunkt befinder sig på x-aksen
|
| Hvis d > 0 |
To løsninger: parablens to rødder skærer begge x-aksen
|
|
Hvis d < 0
|
Ingen løsninger: ingen af parablens rødder skærer x-aksen
|
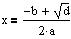
|
Første løsning
|
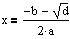
|
Anden Løsning
|

