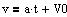 |
Hastighedsfunktionen for
en bevægelse med konstant acceleration a og begyndelsessted v
0. |
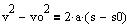 |
Sammenhængen mellem
hastighed og sted for en bevægelse med konstant acceleration a, begyndelseshastighed v
0 og begyndelsessted s0. |
| Bevægelses i homogen kraftfelt |
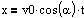 |
|
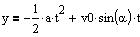 |
Stedkoordinaterne for
en plan bevægelse med konstant acceleration. Accelerationen har størrelsen
a og er rettet i y-aksens negative retning. Begyndelseshastigheden er i
x-aksens retning v0*sin(a). Begyndelsesstedet er (0m, 0m). |
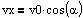 |
|
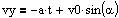 |
Hastighederne i
henholdsvis x-aksens retning og y-aksens retning for en plan bevægelse med
konstant acceleration. Accelerationen har størrelsen a og er rettet i y-aksens negative retning. Begyndelseshastigheden er i
x-aksens retning v0*cos(a), og i y-aksens retning v0*sin(a). |
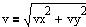 |
Farten i en plan
bevægelse, når hastigheden i x-aksens retning er vx, og i y-aksens retning
vy. |
| Periodisk bevægelse |
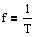 |
Sammenhængen mellem frekvensen f og perioden T for en periodisk bevægelse. |
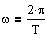 |
Sammenhængen mellem
vinkelhastigheden w og perioden T for en periodisk bevægelse.
|
| Harmonisk bevægelse
|
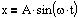 |
Stedfunktionen for en
harmonisk bevægelse. Det største udsving A kaldes amplituden. Bevægelsen kan også beskrives ved en
cosinusfunktion. |
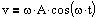 |
Hastighedsfunktionen
for en harmonisk bevægelse med stedfunktionen x=A*sin(w*t)
|
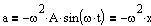 |
Accelerationsfunktionen
for en harmonisk bevægelse med stedfunktionen x=A*sin(w*t).
|
| Cirkelbevægelse med konstant fart
|
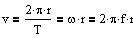 |
Størrelsen af farten i
en cirkelbevægelse med radius r, omløbstid T, konstant vinkelhastighed w
og frekvens f.
|
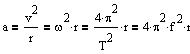 |
Størrelsen af accelerationen i en cirkelbevægelse med radius r,
konstantfart v, vinkelhastighed w, ømløbstid T og frekvans f.
|
| Kraft og arbejde
|
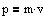 |
Impulsen af en partikel
med massen m og hastigheden v.
|
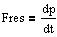 |
Newtons anden lov.
Den resulterende kraft er med tilnærmelse middelværdien af impulsændring pr. tidsenhed.
|
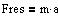 |
Fres er den
resulterende kraft på en partikel med massen m og acceleration a.
|
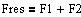 |
Hvis to enkeltkrafter
på en partikel har samme retning, er størrelsen af den resulterende kraft summen af de to enkeltkræfters størrelse.
Hvis kræfterne er modsat rettede, er størrelsen af den resulterende kraft differensen mellem de
to enkeltkræfters størrelse. Hviskræfterne ikke er paralelle, bestemmes størrelsen og retning af den resulterende kraft ved hjælp af
kræfternes paralellogram.
|
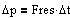 |
Dp er tilvæksten i partiklens impuls,
når partiklen påvirkes af en konstant resulterede kraft Fres i tidsrummet.
|
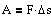 |
A er det arbejde, som en konstant kraft F udfører på en partikel,
der forskydes strækningen D s i kraftens retning.
Det arbejde, som en varierende kraft F udføre på en partikel under forskydning fra
s1 og s2, kan beregnes som arealet under (s,F)-grafen s=s1 tils=s2.
|
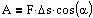 |
A er det arbejde, som en konstant kraft F udføre på en partikel,
der forskydes D s i en retning, der danner vinklen
a med kraftens retning.
|
| Arbejde og energi
|
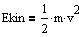 |
Den kinetiske energi af en partikel med massen m og hastigheden v.
|
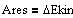 |
Den resulterende krafts arbejde er lig tilvæksten af partiklens kinetisk energi.
|
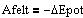 |
Når en partikel
forskydes i et konservativt kraftfelt, er det arbejde, feltkraften udfører på partiklen, lig minus tilvæksten af partiklens potentielle energi.
|
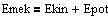 |
Den mekaniske energi er summen af den kinetiske energi og den potentielle energi.
I et isoleret mekanisk system uden gnidning er den mekaniske energi bevaret.
|
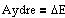 |
De ydre kræfters arbejde på et system er lig tilvæksten af systemets energi.
|
| Effekt
|
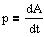 |
P er den effekt, hvormed arbejdet A udføres.
Effekten kan med tilnærmelse beregnes som P=D
A/DT.
|
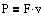 |
P er den effekt, hvormed kraften F udfører arbejde på en partikel, når
partiklen har hastigheden v i kraftens retning.
|
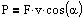 |
P er den effekt, hvormed energien E omsættes. Effekten kan med
tilnærmelse beregnes som P=DE/Dt.
|
| Stød
|
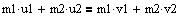 |
Impulsbevarelsessætningen
for et centralt stød. Et stød er centralt, når partiklerne bevæger sig
langs samme rette linie før og efter stødet.
|
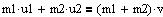 |
Impulsbevarelsessætningen
for et centralt, fuldstændig uelastisk stød. Et stød er fuldstændig
uelastisk, når partiklerne følges ad efter stødet.
|
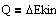 |
Q-værdien for en proces er tilvæksten af den kinetisk energi under
processen. Et sammenstød kaldes elastisk, når Q-værdien for stødprocessen er 0 J.
|
| Tyngdekraft |
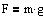 |
F er størrelsen af tyngdekraften på et legme med massen m et sted,
hvor tyngdeaccelerationen er g.
|
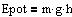 |
Epot er den potentielle enrgi af en partikel med massen m i højden
h over nulpunktet i et homogent tyngdefelt.
|
| Gravitation |
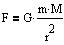 |
F er størrelsen af gravitationskraften mellem to partikler med masserne
m og M i afstanden r fra hinanden.
|
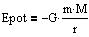 |
Epot er den potentielle energi af to partikler med masserne m og
M i afstanden r fra hinanden, som påvirker hinanden med gravitationskraften.
|
| Elastisk kraft
|
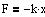 |
En kraft er elastisk, hvis den er rettet mod et bestemt punkt, ligevægtsstillingen,
og dens størrelse er proportional med afstanden x fra ligevægtsstillingen. Konstanten k kaldes fjederkonstanten eller
stivheden.
|
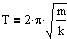 |
T er svingningstiden for en partikel med massen m, der er påvirket
af en elastisk kraft med fjederkonstanten k.
|
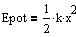 |
Epot er den potentielle energi af et elastisk system med fjederkonstanten
k, idet nulpunktet for den potentielle energi er i ligevægtsstillingen.
|
| Gnidning |
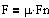 |
Størrelsen af gnidningskraften mellem faste, tørre flader, der bevæger sig i
forhold til hinanden. Fn er størrelsen af normalkraften, og m er gnidningskoefficienten.
|
| Tryk og densitet
|
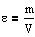 |
Densiteten e af et stof er massen pr.
rumfangsenhed
|
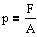 |
Trykket p er kraften pr. arealenhed.
|
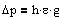 |
Dp er trykbidraget fra en
væske eller en gas med densiteten d stykket h under overfladen.
|
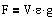
|
F er størrelsen af opdriften på et legme, der fortrænger
rumfanget V af en væske eller en gas med densiteten d.
|
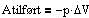 |
Atilført er det arbejde, der tilføres et system ved en process,
hvorunder systemets volumen vokser med DV, mens trykket p er konstant.
Arbejdstilførelsen ved
volumeændring fra V1 til V2, når trykket variere, kan beregnes af arealet under (V,p)-grafen fra V=V1 til
V=V2.
|
| Ideal gasser
|
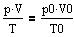 |
Sammenhængen mellem trykket p, rumfanget V og kelvintemperaturen
T af en afspærret mængde af en idealgas.
|
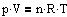 |
Tilstandsligningen for
en afspærret mængde af en idealgas. n=m/M er stofmængden angivet i mol, M er gassens molare masse, og R er
gaskonstanten.
|
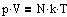 |
Tilstandsligningen for en afspærret mængde af en idealgas, der indeholder N
molekylse. k er Boltzmanns konstant.
|
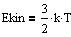 |
Ekin er middelværdien af et et atoms kinetiske energi i en énatomig
idealgas med kelvintemperaturen T.
|

